Introduzione al concetto di Bayesiano

Il concetto di Bayesiano, nel campo della probabilità e dell’inferenza statistica, ruota attorno al teorema di Bayes, un’idea fondamentale che ci aiuta a comprendere come aggiornare le nostre credenze alla luce di nuove informazioni.
Il teorema di Bayes e il suo ruolo nella probabilità
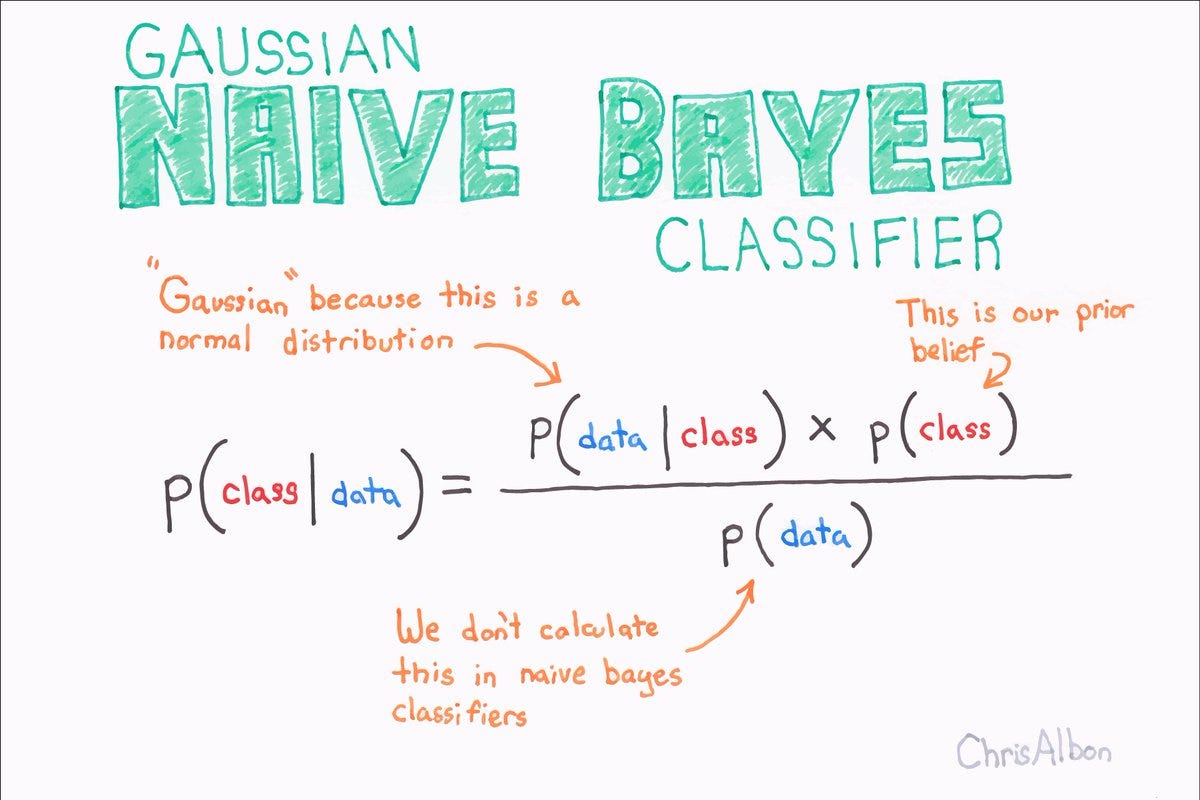
Il teorema di Bayes fornisce una formula per calcolare la probabilità di un evento, data la conoscenza di un altro evento correlato. In altre parole, ci permette di aggiornare la nostra probabilità iniziale (detta “probabilità a priori”) di un evento, considerando nuove informazioni o prove (dette “probabilità condizionata”). Il teorema di Bayes può essere espresso come segue:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità di A dato che B è accaduto.
* P(B|A) è la probabilità di B dato che A è accaduto.
* P(A) è la probabilità a priori di A.
* P(B) è la probabilità a priori di B.
L’approccio bayesiano all’inferenza statistica
L’approccio bayesiano all’inferenza statistica si basa sul teorema di Bayes. Invece di cercare di confutare un’ipotesi nulla, come nell’approccio frequentista, l’approccio bayesiano cerca di aggiornare la nostra probabilità a priori di un’ipotesi, considerando i dati osservati. In altre parole, l’approccio bayesiano considera la probabilità di un’ipotesi alla luce dei dati disponibili, mentre l’approccio frequentista si concentra sulla probabilità dei dati, data un’ipotesi.
Differenze chiave tra l’approccio bayesiano e quello frequentista
L’approccio bayesiano e quello frequentista differiscono in diversi modi fondamentali:
* Interpretazione della probabilità: L’approccio frequentista interpreta la probabilità come la frequenza relativa di un evento in un numero infinito di prove. L’approccio bayesiano, invece, interpreta la probabilità come una misura del grado di fiducia in un evento, basata sulle informazioni disponibili.
* Trattamento delle ipotesi: L’approccio frequentista cerca di confutare un’ipotesi nulla, mentre l’approccio bayesiano cerca di aggiornare la probabilità a priori di un’ipotesi, considerando i dati osservati.
* Utilizzo delle informazioni a priori: L’approccio bayesiano incorpora le informazioni a priori, ovvero le conoscenze precedenti su un evento, nell’analisi. L’approccio frequentista, invece, non considera le informazioni a priori.
Applicazioni del pensiero bayesiano
Il pensiero bayesiano, come abbiamo visto, offre un potente strumento per aggiornare le nostre credenze alla luce di nuove informazioni. Questo approccio trova applicazioni in diversi campi, dalla medicina alla finanza, dall’intelligenza artificiale alla scienza forense.
Esempi di applicazioni del pensiero bayesiano
Il pensiero bayesiano viene utilizzato in una varietà di contesti per risolvere problemi complessi e prendere decisioni informate. Ecco alcuni esempi concreti:
- Medicina: Il pensiero bayesiano viene utilizzato per diagnosticare le malattie. Ad esempio, un medico può utilizzare la probabilità a priori di una malattia in una popolazione, insieme ai risultati dei test diagnostici, per stimare la probabilità che un paziente abbia quella specifica malattia. Questo approccio aiuta i medici a prendere decisioni più accurate e informate.
- Finanza: Il pensiero bayesiano viene utilizzato per analizzare i dati finanziari e prevedere i movimenti dei mercati. Ad esempio, i gestori di portafoglio possono utilizzare il pensiero bayesiano per stimare la probabilità di successo di un investimento, considerando i dati storici e le condizioni attuali del mercato.
- Intelligenza artificiale: Il pensiero bayesiano è alla base di molti algoritmi di apprendimento automatico. Ad esempio, i filtri antispam utilizzano il pensiero bayesiano per identificare e bloccare i messaggi di posta indesiderati. Le reti bayesiane, un tipo specifico di modello grafico probabilistico, vengono utilizzate per modellare le relazioni tra variabili e per inferire le probabilità di eventi futuri.
Tabella delle applicazioni del pensiero bayesiano
La seguente tabella mostra alcune applicazioni del pensiero bayesiano in diversi settori:
| Settore | Applicazione |
|---|---|
| Medicina | Diagnosi delle malattie, sviluppo di nuovi farmaci |
| Finanza | Gestione del rischio, previsione dei mercati |
| Intelligenza artificiale | Apprendimento automatico, visione artificiale, elaborazione del linguaggio naturale |
| Scienza forense | Analisi delle prove, identificazione dei sospettati |
| Meteorologia | Previsioni meteorologiche |
| Marketing | Segmentazione dei clienti, targeting delle campagne pubblicitarie |
Vantaggi e svantaggi dell’approccio bayesiano
L’approccio bayesiano presenta diversi vantaggi:
- Aggiornamento delle credenze: Il pensiero bayesiano consente di aggiornare le nostre credenze alla luce di nuove informazioni, rendendo il processo decisionale più flessibile e adattivo.
- Gestione dell’incertezza: L’approccio bayesiano è in grado di gestire l’incertezza in modo esplicito, fornendo una misura quantitativa del grado di fiducia nelle nostre conclusioni.
- Modellazione di relazioni complesse: Le reti bayesiane, un esempio di applicazione del pensiero bayesiano, permettono di modellare relazioni complesse tra variabili, offrendo una visione più completa dei sistemi in esame.
Tuttavia, l’approccio bayesiano presenta anche alcuni svantaggi:
- Dipendenza dalle probabilità a priori: La scelta delle probabilità a priori può influenzare significativamente i risultati dell’analisi bayesiana. Se le probabilità a priori sono inaccurate, le conclusioni possono essere distorte.
- Calcoli complessi: L’applicazione del pensiero bayesiano può richiedere calcoli complessi, soprattutto quando si tratta di modelli con molte variabili.
- Disponibilità dei dati: L’approccio bayesiano richiede un’ampia quantità di dati per ottenere risultati affidabili. Se i dati sono limitati o di scarsa qualità, le conclusioni possono essere poco accurate.
Modelli bayesiani e tecniche

I modelli bayesiani offrono un framework potente per l’analisi dei dati, consentendo di integrare la conoscenza pregressa con i dati osservati per ottenere inferenze più accurate. Questo approccio si basa sul teorema di Bayes, che definisce la probabilità di un evento in base a informazioni precedenti.
Tipi di modelli bayesiani
I modelli bayesiani possono essere classificati in diversi tipi, ciascuno con caratteristiche e applicazioni specifiche. Tra i più comuni:
- Modelli lineari bayesiani: estensione dei modelli lineari tradizionali che incorporano una distribuzione di probabilità sui coefficienti del modello. Questo consente di ottenere inferenze più robuste e di gestire la presenza di dati mancanti o outliers.
- Reti bayesiane: modelli grafici che rappresentano le relazioni di dipendenza tra variabili attraverso un grafo diretto aciclico. Ogni nodo del grafo rappresenta una variabile, e gli archi rappresentano le dipendenze tra le variabili. Le reti bayesiane sono utilizzate per modellare sistemi complessi con molte variabili interdipendenti.
- Modelli gerarchici bayesiani: modelli che utilizzano una struttura gerarchica per modellare la variabilità tra diversi gruppi di dati. Questo tipo di modello è particolarmente utile quando si hanno dati raccolti da diverse fonti o gruppi.
- Modelli non parametrici bayesiani: modelli che non assumono una forma specifica per la distribuzione di probabilità dei dati. Questo consente di modellare dati complessi con strutture non lineari o con un numero elevato di variabili.
Tecniche di inferenza bayesiana
L’inferenza bayesiana mira a stimare la distribuzione di probabilità dei parametri del modello, dato i dati osservati. Le tecniche di inferenza bayesiana più comuni sono:
- Inferenza MCMC (Markov Chain Monte Carlo): un metodo di simulazione che genera campioni dalla distribuzione posteriore dei parametri del modello. Questo metodo è versatile e può essere applicato a una vasta gamma di modelli bayesiani.
- Approssimazione variazionale: un metodo che approssima la distribuzione posteriore con una distribuzione più semplice, come una distribuzione gaussiana. Questo metodo è più efficiente dell’inferenza MCMC, ma può essere meno preciso.
Risorse e strumenti
Esistono numerosi strumenti e risorse disponibili per l’implementazione di modelli bayesiani:
- Librerie software: R, Python (PyMC3, Stan), JAGS, BUGS
- Pacchetti software: WinBUGS, OpenBUGS
- Libri e articoli scientifici: “Bayesian Methods for Data Analysis” di Andrew Gelman et al., “Doing Bayesian Data Analysis” di John Kruschke
- Community online: forum, blog, siti web specializzati
Bayesian methods, with their focus on updating beliefs based on new evidence, can be applied to various fields, including finance. One example is the analysis of investment strategies, where Bayesian models can help assess the potential impact of investments, such as those made by Invoke Capital , on market performance.
By incorporating prior knowledge and adjusting probabilities as new data becomes available, Bayesian analysis can provide valuable insights into the dynamics of capital allocation and its effects on financial markets.
Bayesian methods, with their emphasis on updating beliefs based on new evidence, can be applied to understanding the complex world of business. A successful entrepreneur, often referred to as a tycoon , is a master of adapting their strategy based on market shifts and customer feedback.
In this way, Bayesian thinking can be seen as a powerful tool for navigating the uncertainties inherent in the entrepreneurial journey.
